They baffle, delight and frustrate millions of people around the world every day.
But even the most dedicated Sudoku solver might never have discovered this secret pattern.
Mathematicians have discovered a powerful pattern known as the “Phistomefel Ring” and it is hidden in every Sudoku ever created.
Best of all, puzzle experts say the pattern could help you solve the toughest challenges much faster.
This pattern means that the 16 squares around the center 3×3 ring will always contain the same digits as the 2×2 squares in the corners.
Since this will always be the case in any legitimate Sudoku, you can use this rule to solve otherwise impossible problems.
Professor Sarah Hart, mathematician at Birbeck, University of London and author of ‘Once Upon A Prime’, told MailOnline: ‘If you’re stuck in a diabolical puzzle, knowing some of these equivalent sets can sometimes be the key.’
Below we explain how you can use the pattern to your advantage in your next Sudoku.
Mathematicians have discovered a secret pattern hidden in every Sudoku puzzle called the ‘Phistomefel Ring’, and experts say it could help you solve puzzles faster (file photo)
A Sudoku is a puzzle that involves a 9×9 grid on which numbers one to nine must be placed.
The problem is that each row, column, and 3×3 box must contain each of the numbers one through nine once, and only once.
Satisfying these rules is what makes Sudoku challenging, but it also creates some mathematical patterns that we can exploit.
The Philstomefel ring is just one example of what mathematicians call “set equivalence theory.”
“The basic idea is that in any Sudoku grid there are sets of cells that must contain the same set of numbers,” says Professor Hart.
‘Some of these are part of the definition. Any row contains the numbers 1 through 9 in some order, as does any column, and so does each of the 3×3 blocks. So these are all equivalent sets.’
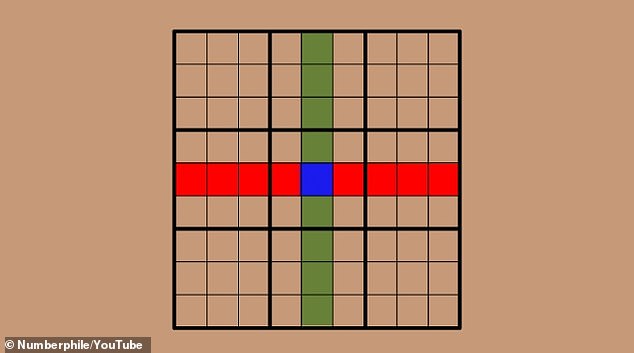
How to explain in this video By YouTuber Numberphile, if we look at the center column and the center row of any Sudoku, we know that they have to have the same set of digits.
Although we don’t necessarily know what order the digits are in, we know that they will both be made up of the digits one through nine.
In a Sudoku, each column, row, and 3×3 box must contain the numbers one through nine, and each number only appears once.
Since the red and green sets must contain the same numbers (1-9), we know that the overlapping square must contribute the same number to each set. If we remove this blue square, that means the sets would still be identical.
So far this may not seem innovative, but things start to get interesting when we look at the points where the two equivalent sets overlap.
The central column and the row have a square in common: the central Sudoku square.
Even if we don’t know what this square is, we know that it contributes the same number to both the vertical and horizontal sets.
If we remove this square, the same number is removed from both and therefore the sets will remain identical.
For example, if the center square is the number ‘9’, by removing this number, both sets would still contain the numbers one through eight in some order.
The point at which this starts to become useful is when we realize that there are larger equivalent sets with even greater overlap.
Professor Hart says: ‘This is a pair of sets of cells containing the same numbers.
“The Phistomefel ring is a very good example of this because it has a beautiful symmetry; the argument involved is a little more complicated.”
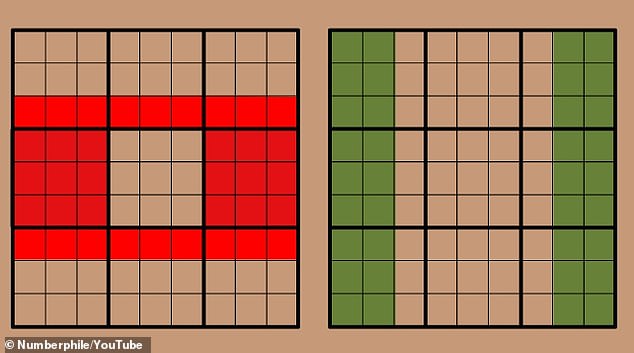
This rule, called “Set Equivalence Theory,” can be applied to larger groups of squares as long as they contain the same number of sets of numbers from 1 to 9. In this diagram, the red and green sets of squares contain exactly the same numbers.
Just as we did with the simple example, we can get rid of the overlapping squares and the remaining red and green squares will still contain identical sets of numbers.
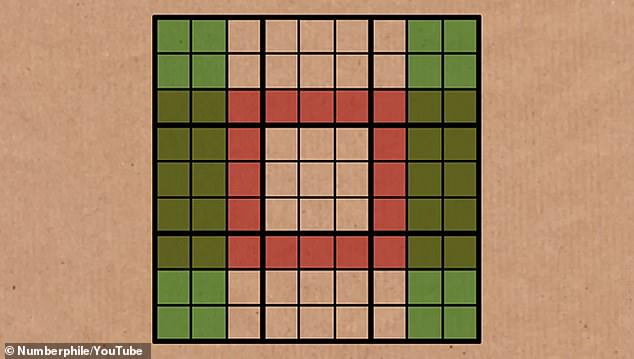
Phistomefel’s ring begins with the rightmost and leftmost two columns of numbers.
These sets are then overlaid on the two 3×3 squares to the left and right of the center block and on the rows directly above and below the center block.
You can see them illustrated more clearly in the diagram above.
We know from the rules of Sudoku that each of these sets must be made up of four lots of digits one through nine arranged in some order.
As in the simple example, we also know that any space where the two sets overlap contributes the same number to each.
So, removing all the overlapping squares, we are left with a center ring of 16 squares and four 2×2 squares in each of the corners that must contain the same digits.
What makes this so useful is that it is true no matter how the Sudoku digits are arranged.
This would be true even if Sudoku did not use numbers but was composed of emojis or letters; If Sudoku is legitimate, the two sets will always contain exactly the same thing.
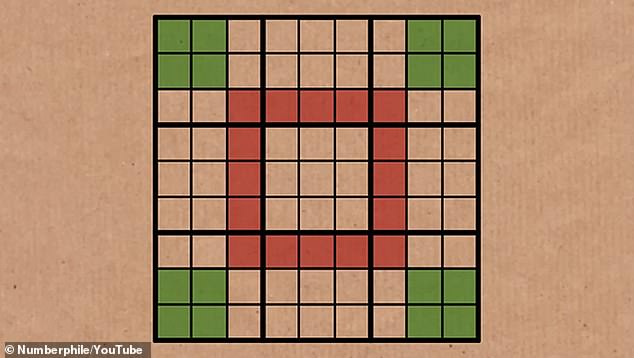
This leaves us with the Phistomefel Ring. Thanks to set equivalence theory we know that the 16 red squares in the middle contain the same numbers as four 2×2 squares around the edges.
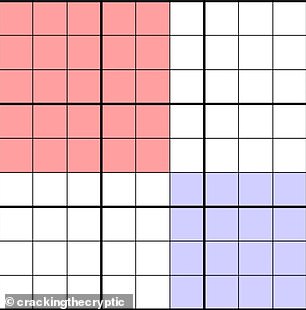
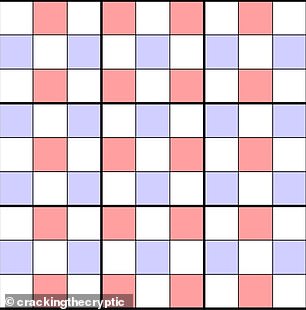
Using these rules, mathematicians and Sudoku builders have identified other equivalent sets (pictured). You can use these rules to quickly solve any Sudoku
“Mathematics is actually about structures and patterns, and that’s why Sudoku puzzles are mathematical,” says Professor Hart.
The Phistomefel Ring is not even the only example of equivalent sets in Sudoku.
Mathematicians and puzzle designers have been able to detect a whole range of simple and complex equivalences.
Professor Hart says knowing these rules can be “another tool in the arsenal” for anyone struggling to solve some puzzles.
“These equivalent sets can be very useful for difficult Sudokus where all the usual methods are useless,” he added.
‘Something like in chess, the more openings, defenses or other stratagems you know, the more options you will have to get out of trouble. ‘


