Perrie Edwards surprised fans by giving a surprise performance on her debut solo song Forget About Us at the song’s listening party on Friday.
After releasing her long-awaited new song, the Little Mix star, 30, took to the stage to perform her song at the event, which was streamed live on Instagram.
Showing off her incredible figure, Perrie stunned in an eye-catching gold halter-neck top and flared jeans during her performance.
Earlier in the day, the blonde beauty also shared the sweet message of support she had received from her Little Mix bandmate Leigh-Anne Pinnock after finally launching her solo career.
Speaking to Greg James on his Radio 1 breakfast show, she said: “Leigh-Anne texted me the other night and said, ‘honey, you look amazing, you’re glowing’ and I said, ‘I miss you so much.’ “. a lot!”

Perrie Edwards surprised fans by giving a surprise performance on her debut solo song Forget About Us at the song’s listening party on Friday.

After releasing her long-awaited new song, the Little Mix star took to the stage to perform her song at the event which was streamed live on Instagram.
‘This is so strange. I look to my right, I look to my left and they’re not there. And I’m like, “This is really weird because we’ve been living in each other’s pockets, 24/7 for 12 years, that’s a long time!”
As soon as Perrie’s single was released, it sent fans into a frenzy, with some declaring the song “a masterpiece.”
The singer who collaborated with Ed Sheeran on the song saw her stunning vocals branded the “voice of a generation” when the catchy tune hit No. 1 on UK iTunes within hours of its release.
Perrie has ditched her last name as she embarks on her solo career with her first song, which includes a yet-to-be-released video directed by Beyoncé collaborator Jake Nava, and is already leaving fans “obsessed.”
On It’s an early summer bop’: ‘Perrie Edwards is the best vocalist of my generation.’
‘Perrie Edwards really wanted her first single to be a hit! Never in my life have I loved a song for the first time…until now! Oh my god’: ‘Perrie Edwards, your voice, baby!’ : ‘I’m literally obsessed’: ‘THIS SONG IS A MASTERPIECE MY QUEEN’.
‘Wow, Forget About Us is number 1 on iTunes UK and the lyric video is number 2. I’m so proud of you Perry!! Congratulations!!’: ‘This song is SO GOOD, Perrie and Ed Sheeran and whoever else helped write this song did a brilliant job, can’t wait for the next single’: ‘Perrie deserves so, so much!’ ‘So happy for her!!’
Perrie is following in the footsteps of former bandmates Leigh-Anne Pinnock and Jesy Nelson going solo.
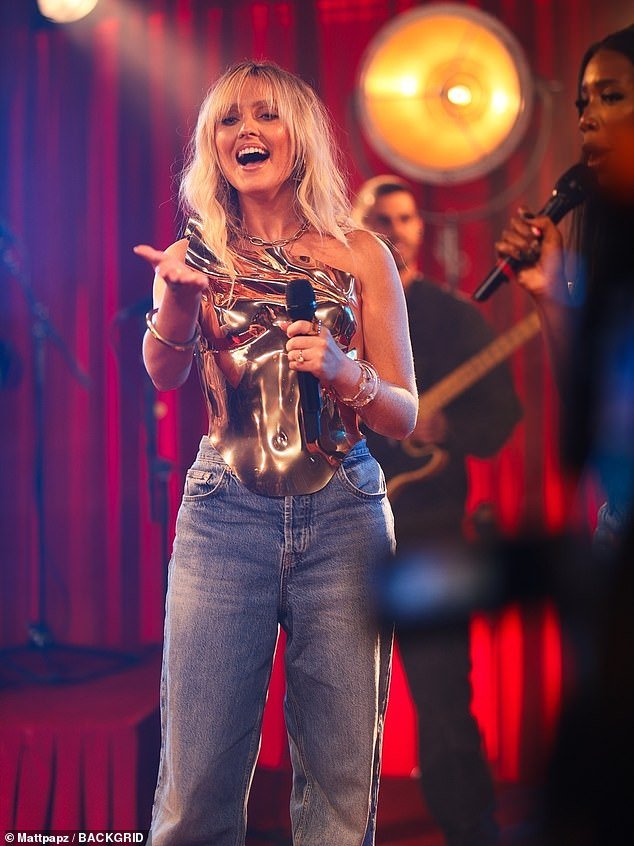
Showing off her incredible figure, Perrie stunned in an eye-catching gold halter-neck top and flared jeans during her performance.

Earlier in the day, the blonde beauty also shared the sweet message of support she had received from her Little Mix bandmate Leigh-Anne Pinnock (pictured from the 2022 tour).

As soon as Perrie’s single was released, it sent fans into a frenzy, with some declaring the song “a masterpiece.”
And the singer, who was previously engaged to Direction’s Zayn Malik before footballer Alex Oxlade-Chamberlain revealed the new song was inspired by her past, saying: “I look back at past relationships and think happily of those moments.”
‘Do I want to be there now? No. It didn’t work out that way and if it was supposed to, it would have happened. “Relationships have been a big part of my life and have made me who I am today.”
Before adding: “I think it’s a nice feeling to be honest and it’s very relatable.”
Perrie, who shares her two-year-old son Axel with her fiancé Alex, said her next album would also include rock and roll, country and disco influences.
“Going to solo sessions now and being able to say what I want and feel is the most incredible experience.”
She continued, “I’ve never had the confidence to do that before, but this process has allowed me to believe in myself and explore all of my different emotions and different parts of my life.”
Most of the album was recorded at their north London home after Alex suggested they convert their disused dining room into a home studio.
She confessed: ‘I am very proud of what I have done and created. I wanted it to be fun more than anything else and showcase my singing through ballads and big vocal numbers.
Before revealing his plans to tour with a live band: ‘Having people singing your songs is the best natural high in the world. “I’m really excited to see how fans react to my music now.”
While the musician co-wrote Forget About Us with Ed, 33, he also announced that the duo had collaborated for a second song.
Perrie explained: ‘I feel like all the collaborations happened organically. With Ed Sheeran, he had a song, he called me and we discussed the concept.”
She continued, “I loved the melody, I loved the vibe; I admire him so much that I think he’s one of the most talented human beings out there.”
“She’s also such a nice, genuine person, so I felt comfortable saying, ‘I love it, but conceptually it’s not me. I’m not at that stage in my life right now. Would you be okay if I modified the lyrics to fit me and my life?”

Perrie has ditched her last name as she embarks on her solo career with her first single, which includes a yet-to-be-released video directed by Beyoncé collaborator Jake Nava, and is already leaving fans “obsessed.”

Most of the album was recorded at her north London home after her fiancé Alex Oxlade-Chamberlain suggested turning her disused dining room into a home studio (pictured with her two-year-old son Axel).
And he said, “Of course!” He wanted me to have full ownership of it, so I went and did it.
Formed on The X Factor in 2010, Little Mix enjoyed enormous success throughout their 11-year recording career before announcing their split in December 2021.
But the bandmates have suffered mixed fortunes since confirming their decision to leave the band to pasture.
Former member Jesy, who left the band in 2020 to prioritize her mental health, originally signed a solo deal with Polydor Records.
The two parted ways with the label in 2022 following a lukewarm response to their debut single, Boyz.
The singer later released his second solo single, Bad Thing, independently, but the song failed to enter the UK Top 100 Singles Chart.
Jesy has since scrapped her plans to release third single Cried Out in favor of a “quick banger” which she says is “me in a nutshell”, according to sources.
Speaking to The Mirror, a source said: ‘Jesy has been listening to her critics. She’s desperate to give fans something epic and she’s doing her best to find her authentic sound, but the sudden change has destabilized her side.
“Last year, it was believed that most of her debut album was finished – even the artwork was in place – but since then Jesy has made a big U-turn and everything is being reworked, even the aesthetics, as she doesn’t matches their new album. -tempo direction.’
In 2022, Leigh-Anne signed her own solo deal with Warner Records and released the debut single Don’t Say Love in June 2023.
